Wringing out the risks

By Keith Button|March 2018

Mathematicians are exploring an entirely new approach to making aircraft safer

The chances of failure for complex aerospace systems, such as a helicopter, are so extremely small that it’s difficult for designers to understand the unlikely confluence of circumstances that leads to failure. These systems exhibit an “average behavior” of high reliability, which is why “plane crashes happen very infrequently,” explains applied mathematician Tuhin Sahai, a Berkeley, California-based associate director of United Technologies Research Center in Connecticut.

The current method for simulating and predicting failure requires running computer models millions of times to try to re-create the moment when the system “will do something crazy,” as Sahai puts it. It’s not a very efficient method for wringing out the causes of today’s exceedingly rare failures.

Sahai and his co-principal investigator, applied mathematician Youssef Marzouk of MIT, think they can pinpoint the causes of failures by conducting hundreds of simulations. “All of that stuff is kind of hidden in the model. We’re trying to make the model reveal it to us,” says Marzouk.

They have until April 2019 to prove the technique under a DARPA project called SIRE, short for Scalable Inference for Rare Events. They plan to harness the power of probability and algorithms to define the calculations that would be required for establishing the probability of failure in a complex system and the path to it.

If they succeed, the results could point to safety improvements during design and set the stage for a cockpit alert or intervention system that would stave off dangerous aerodynamic stalls. The SIRE team plans to share its step-by-step recipe with the broader aerospace community, so that other researchers would decide how to apply it.

To define the steps, the SIRE team is starting with two specific cases: aerodynamic stalling in a rotorcraft and power outages in an airplane’s electrical system. Currently, they are building digital models of aircraft electrical systems, adapting their algorithms to accommodate certain dynamic features of the rotorcraft system and building filtering, or estimating, algorithms that will help sense when a system is transitioning into potential failure.

UTRC research engineers are working with the applied mathematicians to build two computer models of electrical systems. One models an electrical current exceeding a threshold in an inductor coil. The other models electrical load instability.

While the research engineers build these models, the SIRE mathematicians are working on filtering algorithms, rare-event simulations and in-flight rare-event prediction algorithms for them. Transient behavior — factors that change over time — will play a key role in the simulated electrical system failures and in predicting those rare events, says Marzouk, who is director of MIT’s Aerospace Computational Design Laboratory.

“It might be that a certain combination of things demanding power — turning on; turning off — conspire to end up overloading some circuit; demanding too much current overall; overloading some power source,” Marzouk says. “We want to understand when things might go catastrophically wrong.”

Marzouk and Sahai communicate regularly via video conferencing, phone and email, and occasionally fly to meet each other. They exchange code via email and run the system simulations on both UTRC and MIT server clusters.

Many of the current algorithms for producing rare-event simulations are limited, either because they make a lot of assumptions about the systems they are applied to or because they’re applied to only one or two dimensions of those systems, Sahai says. Under SIRE, Marzouk and Sahai are adapting concepts not typically combined with rare-event simulations — such as predicting outcomes in the face of uncertain factors and the study of how dynamic systems like the weather behave over time.

Predicting stalls

Marzouk and Sahai are building a model that will digitally represent a helicopter fuselage, tail, blades, shaft and factors such as blade flapping, blade pitching and blade loading. They will introduce random wind gusts that can force a helicopter into a stall, for example, if the blade angle of attack rises above a certain threshold. That can happen faster than a human pilot can react.

The mathematicians want to find the probability of stalling and the conditions that would lead to that failure point. Simulations like these, and understanding how to create them, would help designers of helicopters and other complex systems to build them to better withstand or avoid the conditions that lead to failure. The simulations would not only present the probability of failure, but the exact mechanism or path to failure.

Knowing that path, an engineer could tweak the design for a helicopter to avoid the rare event that will lead to an aerodynamic stall.

Engineers might design the tail rotor for stability in cruise and hover conditions, and with the thinking that the rotorcraft will need to withstand wind gusts of a certain magnitude, Marzouk says. But sometimes a larger gust occurs, or a sequence of small wind gusts or other factors affecting the system can occur immediately after each other, to cause a stall.

Today, Marzouk says, “you might design [the helicopter] to respond to certain kinds of input, but there might be strange inputs or strange changes to the system, or things you haven’t modeled correctly that conspire to give you bad behavior.”

Marzouk and Sahai are also estimating the probability of stalling, in real time, for a computer-simulated rotorcraft system as it flies. In the future, a variation of this real-time failure prediction model might be loaded into an onboard computer to help helicopter pilots in midflight assess the risks of flying through bad weather.

“You can constantly update your probability of failure and decide whether you want to continue with the mission or you want to go land somewhere,” Sahai says. Or, a failure prediction program could be paired with a digital look-up table to tell the helicopter pilot or the aircraft what to do in specific situations.

Another option could be “some kind of automated system that intervenes faster than the human could,” Marzouk adds.

He and Sahai are creating a simplified computer model to predict how the system would behave so the model can spit out its predictions in real time. The model would be updated with information about the current state of the simulated rotorcraft system — information that sensors would provide if the simulation were a real-world flight.

Building on existing models

One hurdle Marzouk and Sahai had to overcome in working on both rotorcraft scenarios was in modifying filtering algorithms that estimate the current states of complex systems. Filtering algorithms are common in aerospace applications, filtering out noise to produce a clear signal, for example.

Marzouk and Sahai adapted these algorithms to track the probability of system failure instead of the overall expected behavior of the system.

Instead of focusing the filtering algorithms on the peaks of distribution of possible outcomes — the most common outcomes — the mathematicians focused them on the tails of the distribution, or the rare events.

Conventional filtering algorithms had to be tweaked, because they don’t do well at capturing rare transitions, or predicting when the next step will lead to a rare event, Marzouk says. If the data from the system reflects a one-in-a-million phenomenon, the filter will almost always ignore the data.

“Most filtering algorithms are essentially going to say: ‘My model says 999,999 times out of a million this is not going to happen, so, look, data, you’re noisy; you’re an outlier; my prediction is that things are just fine.’” Those are exactly the rare events that Marzouk and Sahai want their algorithms to home in on.

A lot of the filters fail to show the true structure of tail distributions — the low-probability events — because they make approximations based on standard bell-curve probability distributions, Marzouk says. For their real-time stall-estimating algorithms, the mathematicians are building on ideas from large-deviations theory, which characterizes tail distributions, the shapes of those tail distributions and how the probabilities change for events as those events become more and more rare.

Marzouk and Sahai are also building on variational filtering algorithms. These are filtering algorithms that take an optimization approach, so that mathematicians can “push toward probability distributions that are weird, or not what you would have expected,” Marzouk says.

“That is exactly what you want to be able to do when the data come in and tell you the system has done something unexpected. You want the algorithm to be able to actually find those distributions that reflect the unexpected thing,” he says.

Like a living system

Another problem for the mathematicians is the dynamical nature of the rotorcraft system, meaning that it has inertia and momentum. A dynamical system has its own intrinsic time scale, so it may not react to a change immediately, but it may evolve over time. Marzouk compares it to a living thing, and says it’s much more difficult to predict its rare events than those of a static system.

“If you kick it, it won’t just immediately deform; it might oscillate back and forth for a while after you kick it, and maybe those oscillations will dampen out after a while because of the intrinsic dynamics of the system,” Marzouk says. “Events that have accumulated in the past might conspire to put you in a bad situation currently, even if none of those individually in a static analysis would have looked bad.”

For the rotorcraft system, for example, the fact that it may have experienced a series of 10 wind gusts may not make a difference if each gust is analyzed individually, but the direction of the gusts and how long each one lasted may make a difference when the 11th gust comes along, Marzouk says.

The mathematicians need to push the computer-simulated rotorcraft system, computationally speaking, into rare events so they can accurately estimate the probability of failure. But rotorcraft systems are designed to be stable, so even when the system is disturbed, its dynamics tend to push it back into its normal operating range. That’s a good feature for a rotorcraft system to have, but it makes it challenging for the mathematicians to push the system into failure, Sahai says.

“You want the system to fail computationally,” he says. “If the system doesn’t fail, then you don’t have a good estimate of the probability of failure.”

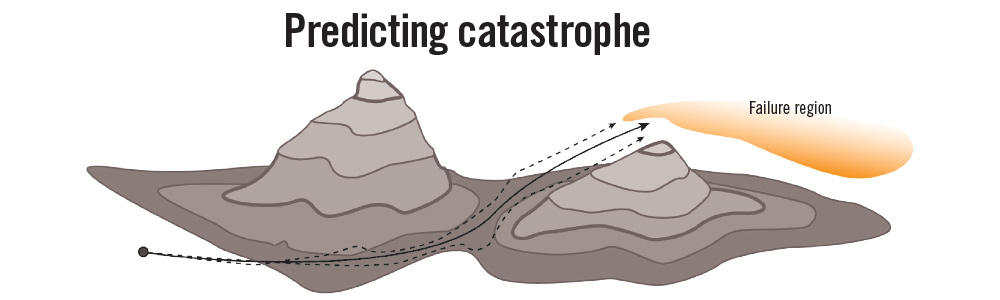
Another challenge was how to organize and visualize the data. They have defined probability spaces containing 12 to 15 variables, which means these theoretical spaces must have 12 to 15 dimensions. For the rotorcraft model, the dimensions include the rotor blade’s angle of attack, its pitch rate, the x-direction velocity and the z-direction velocity. The mathematicians typically visualize the multiple dimensions through lines of figures in a table, or a map plotted with only two or three dimensions at a time, Sahai says. A blob in the probability space represents the failure region, or collective points of failure, and the job of Marzouk and Sahai is to compute the most likely path between the current point of operation and failure.

“There’s a certain rule in rare-event simulation: The likeliest path to failure is the one you normally take,” Sahai says. “That is the path that will dominate all of the other paths.”

The complexity of the rare-event distributions within the probability space, which can be “weird and skewed,” makes them difficult to reach, Sahai says. One concept that Marzouk and Sahai are adopting to attack this issue is the transport map. The mathematicians simplify the rotorcraft system’s distribution to make it easier to fail, then they select a transport map — a mathematical object — that morphs the more normal distribution back to the original, complex distribution. Each system’s transport map is unique, but the same mathematical approach to selecting the transport maps can be adopted for different systems. That means the steps the mathematicians build to select the transport map for the rotorcraft system will be the same for the electrical system, and these steps can create transport maps for other complex systems.