Imaging a habitable world

January 2019

Scientists are detecting exoplanets daily by the slight decrease in light from a host star as a planet transits in front of it. Photos of such a planet could tell us whether or not we are alone in the universe. Louis D. Friedman and Slava G. Turyshev think they have a solution for delivering this photographic evidence, one that will require a 900 trillion-kilometer journey and applying a phenomenon discovered by Einstein.

Epiphany can be a hyperbolic word, but while co-leading a Keck Institute for Space Studies study four years ago, Lou had a genuine one.

Lou knew intellectually that there are no targets of interest in terms of searching for life in the universe between where the Voyager 1 spacecraft is now (approximately 145 astronomical units or 21.7 billion kilometers from Earth) and Alpha Centauri, the nearest star to our own, 4.37 light years (276,000 AU) away. Viewing a graphic of mostly empty space made the problem visceral. How could humanity ever hope to reach across such a vast void to learn meaningful details about exoplanets, including whether they harbor life? We were familiar with the renewed dream of interstellar space flight, because we are members of the advisory committee for the privately funded Breakthrough Starshot Initiative, which seeks to send a robotic interstellar probe through the Alpha Centauri system. As enthusiastic as we are about this long-term interstellar vision, its realization may be centuries away, at least.

Lou’s epiphany was to see that we could set an intermediate objective of sending a telescope to a region outside our solar system and photograph an exoplanet from there. Slava briefed the Keck Institute for Space Studies, or KISS, study group about this idea for studying exoplanets not only in the Alpha Centauri system but much farther beyond and much sooner. We will be refining the concept this year and next under a two-year NASA Innovative Advanced Concepts Phase 2 grant of $500,000 awarded last year.

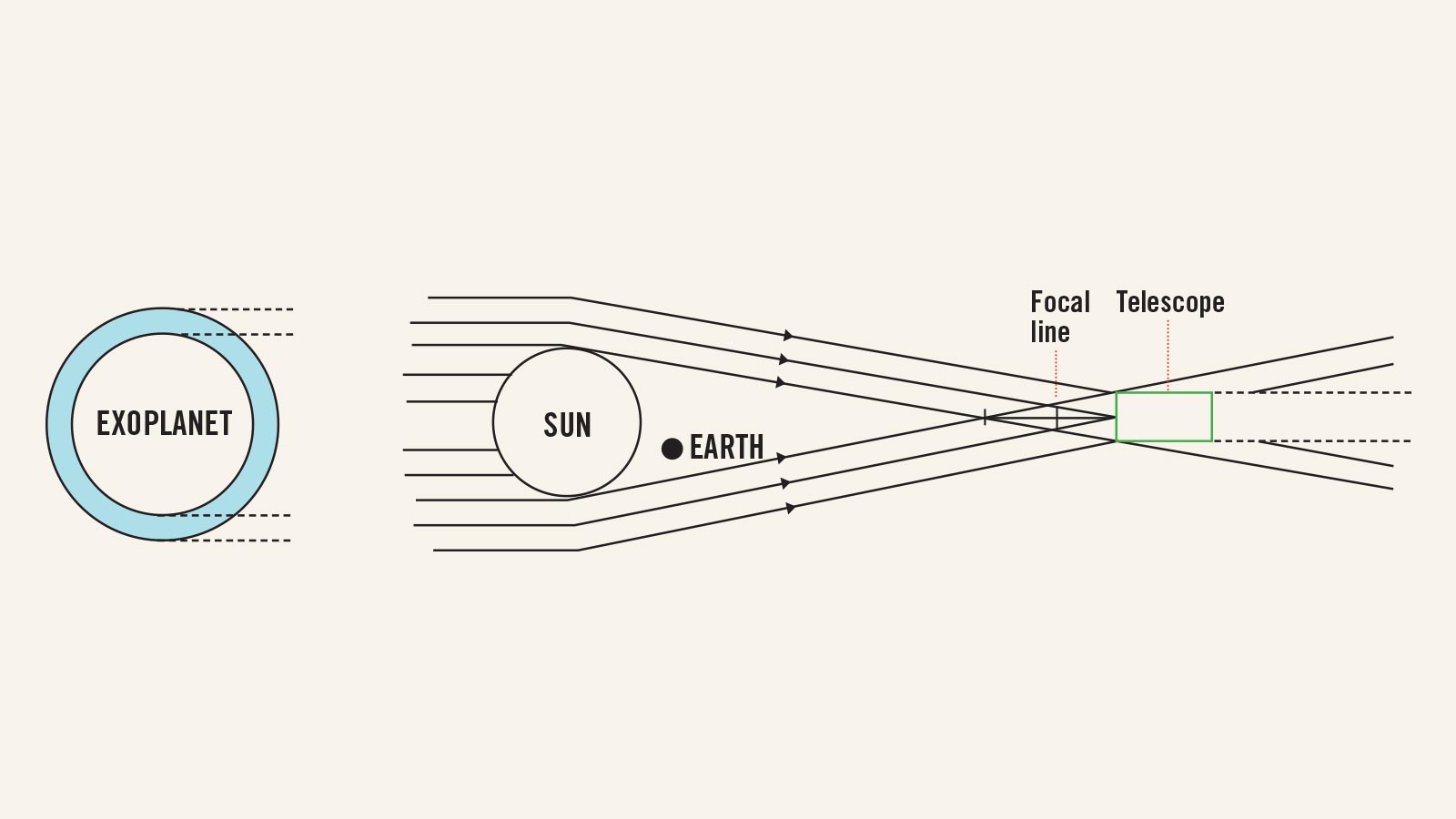
We owe the origins of the idea to Albert Einstein. Just as Einstein predicted, the sun’s gravity field bends light rays to provide a natural lens with the power to magnify light from distant objects by a factor of about 100 billion times. To put this phenomenon to work, we would begin by identifying a promising, potentially habitable exoplanet in data from either the Kepler space telescope or TESS, the Transiting Exoplanet Survey Satellite, or those found by other exoplanetary surveys. We would observe them from Earth to confirm the best habitable candidate. Then, we would send a 1- to 2-meter aperture solar-gravitational telescope on a smallsat to the focal area of the solar gravity lens located beyond 547 AU from the sun. Looking back beyond the sun and toward the exoplanet through the solar gravitational telescope would collect light from the exoplanet after it passes by the periphery of the sun’s photosphere. With this technique, we would achieve a 10-kilometer resolution, fine enough to see continental lines, topography, weather patterns and most intriguingly, signs of civilization, if one exists.

Are there other practical ideas for telescopes that would do this? No. Imaging an exoplanet from space with a conventional lens would require it to be 90-kilometers in diameter, and once erected in space, this lens would have to point at the target for several million years. Even then, it would only acquire just a single picture element — a dot of light — from an exoplanet 100 light years away. That would be impossible with present technology. Another advantage of gravitational lensing is that it would permit years of detailed remote sensing observations of the putative habitable exoplanet at continental scale, rather than gathering at best a few pixels from a fast interstellar fly-by. Our 1-2 m telescope would travel outside our solar system and with small maneuvers follow a trajectory along the focal line, collecting data for many years.

Amazing gift of nature

How does gravitational lensing work? According to Einstein’s General Theory of Relativity, gravity changes the refractive properties of space-time so that light rays no longer move along straight lines. Their paths are bent toward the center of gravity of an object such as the sun. This property of a gravitational field to bend light was confirmed by the famous Eddington experiment conducted during a solar eclipse in 1919. This effect is well understood and is accounted for in tracking of interplanetary and Earth-orbiting spacecraft and used to study the distribution of dark matter in the universe.

As the light from an exoplanet approaches our sun, each part of its wavefront is bent at an angle that is inversely proportional to the distance from that part to the optical axis, an imaginary line connecting the center of the exoplanet to the center of the sun. This angle is rather small, with light rays that just touch the limb of the sun bent by only 1.75 seconds of arc. As a result, after passing by the sun, any two parts of the incident wavefront enveloping the sun from two opposing sides will move toward each other and will ultimately intersect at the optical axis. The rays that move at a larger distance from the sun will intersect farther along the optical axis, forming a focal line. Given the physical size of the sun, the rays begin to intersect at 547 AU, forming a focal region that extends far beyond 2,500 AU.

The parts of the wavefront with similar separations from the optical axis coherently add, thus amplifying the light intensity to a telescope in this region. As seen by an observer at the focal region and because of the azimuthal symmetry of the lens, the light would form a disk around the sun, called an Einstein ring. The larger the distance between a part of the wavefront and the optical axis or, conversely, the larger the radius of the Einstein ring, the farther from the sun the focusing occurs. This gravitational focusing amplifies the photometric intensity, or brightness, by the 100 billion factor and provides a fine angular resolution of a billionth of an arcsecond, another requirement for sharp resolution. This is how the sun acts as a giant lens — our amazing gift from nature.

Technical hurdles

One challenge of gravitational lensing is that light from an exoplanet would be stretched and squeezed while forming the Einstein ring. This spherical aberration would distort the proportions of the original image while admixing the information from adjacent segments on the planetary surface, but the basic features of the exoplanet would still be recognizable. Thus, this problem is surmountable. We know the physical properties of the lens, and so we can recover the original information contained in the images by applying standard image deconvolution techniques. The images would be mathematically broken down into a large number of constituents and reassembled by applying precision mapping algorithms developed with the knowledge of the optical properties of a particular imaging system.

The entire image of an exoplanet situated at, for example, a distance of 100 light years away from us, would be contained with a cylinder with a diameter of about 1.3 km in the vicinity along the optical axis. Thus, a telescope-carrying spacecraft would have to reach the focal region of the solar lens and then continue to move within this cylinder while taking data to form an image.

However, before using the solar lens for imaging purposes, we need to block the light emitted by our sun. A classical coronagraph with a contrast ratio of one part in 10 million is sufficient for this purpose. Given the performance of modern coronagraphs, rejecting this level of solar light does not pose a challenge. In fact, we already have a very robust design for an internal telescope coronagraph that meets the requirements with a significant margin.

We also need to consider the effect of the sun’s corona, or atmosphere, on the light from an exoplanet that passes through it. The brightness of the corona amounts to noise that will make it challenging to detect the faint optical signals of a distant exoplanet. To overcome this difficulty, we need to move sufficiently far from the sun, so that the Einstein ring will become well-separated from the solar disk and the most turbulent part of the corona. Distances beyond 650 AU are well suited for this purpose. This is the distance we must reach to begin the exoplanet imaging. Solar corona will still be present in the data, albeit to a lesser extent, increasing the signal integration time.

Our analysis suggests that with all the effects taken into account, including scattering of light by the ever-present interstellar dust, we could collect enough light in approximately half a year to form the first-ever direct megapixel-class-resolution image of an exoplanet. As nothing is stationary in the universe — the planet orbits its own star, which also moves with respect to our own sun — the spacecraft must have a propulsion system that would compensate for such a motion. If we were limited to conventional imaging by a giant unitary telescope or by multiple telescopes arrayed for interferometry, the telescope or telescopes would have to stare for millions of years to gather enough light.

Also, to assemble the parts of a unitary image, the spacecraft will have to maneuver small distances to capture all the pixels in the Einstein ring. It also will have to compensate for the orbital motion of the target planet and the barycentric rotation of the sun. As hard as those tasks are, they are thousands (if not millions) of times easier than either interstellar flight or the huge (and enormously expensive) task of building kilometer-sized telescopes in space. Fortunately, all the technologies required for such a mission are already in development and flying with their early stages.

Then there is the question of how to get to the focal region in a timely way. The target region of 650 AU is more than four times farther away than Voyager-1, and it took 41 years to reach this distance of 145 AU. This would mean an unacceptable travel time of 182 years. The brute force option calls for sending a large spacecraft to deep space by nuclear electric or nuclear thermal propulsion. This would cut the travel time to perhaps 25 years, but such designs are likely to be politically and economically untenable for the foreseeable future. By contrast, solar thermal or even chemical propulsion could send our notional small telescope within 2 to 4 solar radii of the sun for a gravity assist that would accelerate it enough to exit the solar system and reach the focal area in about 30 years. This, too, would require a large, complex spacecraft with a huge thermal shield. So, we are examining another approach, one that involves thinking small. A smallsat with a mass of, say, 50 kg, and a solar sail measuring 200 x 200 meters, could achieve exit velocities approaching 25 AU/year, depending on the sail material and how close it can get to the sun. We could be gathering light from an exoplanet 26 years after launch. We currently consider approaching the sun to 0.1 AU (21 solar radii) as a reasonable perihelion goal for the solar sail. The solar sail is especially well-suited to the small spacecraft, since its final speed is determined by the area of the sail divided by spacecraft mass. In addition to providing a much lower cost and hence more realizable spacecraft and mission concept, this approach also provides a replicable one, permitting us to consider launching multiple spacecraft to observe multiple targets or to arranging telescopes in distributed architectures that increase reliability, redundancy and mission design flexibility.

The precise size of the smallsat will be dictated by the required telescope size (e.g. , 1-2 meters) and the radioisotope power system requirements. The power system will supply the energy for electric micro-thrusters to enable maneuvering around the focal line as the spacecraft flies outward beyond 650 AU. It will have months and years to observe the target exoplanet, deconvolute the image, and communicate to Earth — a virtual orbiter of the distant exoplanet. It will also be possible to observe whole planetary systems, several exoplanets, orbiting the same star since their focal lines will be relatively close.

Our fellow mission designers at the Aerospace Corporation in California who have joined us in the study, have devised a “string-of-pearls” distributed architecture. They are investigating successive yearly launches of “pearls” (each being a combination of nanosats) that would fly along the target focal line to gather the required light. This would ease the mission design requirements and render technical readiness earlier than would be possible with a single behemoth spacecraft architecture.

No matter which architecture is ultimately chosen, tapping the solar gravitational lens may be our only means to have a high-resolution image of an alien world (and perhaps its putative life) in the foreseeable future — a very sobering realization, one that motivates getting a spacecraft out there. That we can achieve it relatively soon — far earlier than super large space telescopes could be built or interstellar travel achieved, and even with technologies now currently flying in space, brings us ever closer to the goal of finding our analogs, life on another world.

Sending a telescope outside the Earth’s solar system to take advantage of gravitational lensing could give scientists the first close-up view of an exoplanet. The telescope would look toward the sun and collect light from the exoplanet in an Einstein ring (in blue at left) created by the light-bending effect of the sun’s gravity. This gravitational lens could achieve a 10-kilometer-resolution image. Credit: Louis D. Friedman and Slava G. Turyshev

Louis D. Friedman. Credit: Courtesy

Slava G. Turyshev. Credit: Courtesy

This image of Earth was taken at a resolution of 10 to 15 kilometers, similar to the level of detail that could be provided by a telescope positioned to tap the sun’s gravity as a magnifying lens. The photo was taken by NASA’s Earth Polychromatic Imaging Camera, or EPIC, on the Deep Space Climate Observatory, or DSCOVR, satellite. Credit: NASA